Для ознакомления с полноценным материалом, согласитесь и скачайте:
Статья в формате pdfДанная работа продолжает тематику, связанную с фазовыми шумами и синтезом частот. В предыдущей работе было рассмотрено влияние аддитивного шума на сигнал опорной частоты и его преобразование в цифровых делителях. Ниже проведен анализ других источников шума, в том числе фазового детектора, и предложен метод, компенса- циирующий их влияние. Таким образом, продолжается совершенствование и оптимизация существующих решений путем введения новых подходов (по крайней мере с точки зрения реализации), возникающих благодаря развитию современной элементной базы.
Назначением цифровых синтезаторов частот является генерация сигнала или тактовых импульсов произвольной частоты из сигнала фиксированной частоты. Основной особенностью является точное соотношение фаз, а значит и частот, опорного и генерируемого сигнала.
Технология синтеза частот используется в самых различных областях - от измерительного оборудования до средств беспроводной связи и радиолокации. Во многих случаях характеристики используемых синтезаторов являются определяющими при формировании функциональных возможностей и техничесих параметров разрабатываемых систем. Поэтому улучшение характеристик всегда остается актуальной задачей [1, 6].
Существует множество способов построения синтезаторов, например, основанный на переносе частот и переключении смесителей с соответствующими фильтрами, прямой цифровой синтез, основанный на генерации цифровых сигналов sin(x), cos(x) с последующим цифро-аналоговым преобразованием, косвенный метод на основе систем фазовой автоподстройки. Часто используется комбинация перечисленных способов [4].
Каждый из перечисленных методов имеет свои преимущества и недостатки также, как и ограничения, связанные с возможностями элементной базы. Например, для генерации частоты с помощью прямого цифрового синтеза (DDS1) на ряду с ограничением по скорости самой микросхемы, необходима высокая тактовая частота, генерация которой само по себе является не совсем простой задачей, поскольку кварцевые генераторы обладают сравнительно низкой частотой. Сейчас на рынке доступны микросхемы DDS с тактовой частотой до 1GHz, что позволяет произвести выходной сигнал с произвольной частотой до 500 MHz2, минус запас на фильтрацию. Для синтеза более высоких частот используют методы на основе систем фазовой автоподстройки. Эти методы получили на сегодняшний день очень широкое распространение благодаря появлению цифровых фазо-частотных детекторов, позволяющих работать в широком диапазоне частот, и высокоскоростных цифровых делителей, со входной частотой до десятков гигагерц.
Однако, как и у любой физически реализуемой системы, у нее есть свои особенности, влияющие на результирующие характеристики выходного сигнала. Часть из них может быть компенсирована. Анализу и возможному устранению негативного влияния ряда особенностей и посвящена данная работа.
1Direct Digital Synthesis2На первой гармонике. На последующих можно получить и выше, однако в таком случае уменьшается как уровень сигнала, так и его качество
Для рассмотрения характеристик и нахождения способов устранить недостатки необходимо привести систему параметров, на основе которой производится оценка того или иного фактора. Ниже перечислены основные из них.
1.1 Фазовый шум
Фазовый шум является основным критерием качества синтезированного сигнала. Математическое определение было дано в предыдущей работе, здесь лишь напомним, что фазовый шум определен для любого сигнала, образуемого периодической функцией с аргументом, являющимся функцией времени. В случае идеального с нашей точки зрения сигнала эта зависимость является линейной. Производная, т.е. угол наклона, является частотой сигнала. В случае не идеального сигнала частотой является производная, усредненная на достаточно длительном временном окне, а текущее отклонение фазы от произведения частоты на время является фазовым шумом, если рассматривать его как случайный процесс. Единицей измерения спектральной плотности мощности фазового шума является dBc/Hz (де- цибелл относительно несущей на герц), что соответствует 10log[rad2/Hz]. Такая размерность связана прежде всего с методикой измерения фазового шума с помощью спектрального анализа.
1.2 Стабильность
Стабильностью частоты является долговременный уход частоты сигнала от своего номинального (среднего) значения. Относительная стабильность измеряется в миллионных долях, ppm (parts per million), при стабильности выше 1 ppm просто указывается значение, например, ±3 х 10-8. Уход частоты может быть вызван различными факторами - температурой, напряжением питания и т.д.3
Поскольку, как уже было отмечено, фаза4 выходного сигнала точно соотносится с фазой опорного сигнала, то стабильность выходного сигнала полностью определяется стабильностью опорного, т.е. их относительные стабильности равны.
3Обычно под стабильностью подразумевают температурную стабильность. Для характеризации ухода частоты при изменении напряжения питания существует параметр “pushing” [Hz/V], при изменении КСВ нагрузки “pulling’, при старении — “ageing’ [Hz per year]
4Точнее среднее значение приращения фазы за одинаковый промежуток времени при условии входа в синхронизм
1.3 Дипазон перестройки
Одним из параметров, определяющих архитектуру синтезатора является диапазон перестройки частоты выходного сигнала. Существует большой класс задач, где необходим широкий диапазон частот, например, 1:100. Как этого добиться? Управляемых генераторов с таким диапазоном и достаточно линейной характеристикой пока не существует, к тому же при такой характеристике неизбежно возникнут проблемы с устойчивостью. Проблема решается достаточно просто - достаточно изготовить синтезатор с перестройкой в два раза (октавный) в верхнем диапазоне частот, а все остальные частоты получить путем деления на два, четыре, восемь и т.д. Поэтому октавные синтезаторы играют в технике особую роль.
1.4 Минимальный шаг по частоте
Минимальный шаг по частоте - второй параметр, непосредственно влияющий на архитектуру. Он определяет сетку возможных частот выходного сигнала. Дело в том, что входная и выходная частоты связаны соотношением M/N, где M и N - целые числа5 . В зависимости от выбранной архитектуры он может варьироваться от сотен мегагерц до долей герца.
5Возможна генерация и с иррациональными коэффициентами, но на практике используется крайне редко в связи с невысокими характеристиками и сложностью реализации1.5 Предельные характеристики
При оценке фазового шума выходного сигнала возникает вопрос, каковы же теоретические границы, которые невозможно превысить, какие бы усилия не были предприняты. Этот вопрос очень важен, поскольку разработчики часто сбиваются с толку, придумывая новые гибридные схемы синтезаторов и методы компенсации, считая, что получат, например, те же характеристики, что и у качественного опорного генератора, но на более высокой частоте.
Прежде чем ответить на этот вопрос, следует отметить, что есть спектральная плотность мощности фазового шума (функция частоты), а есть интегральная характеристика фазового шума - его мощность, равная интегралу ее плотности6.
Пусть частота опорного сигнала fref, синтезируемая частота fout, Фref(ω) - спектральная плотность фазового шума опорного сигнала (на частоте fref соответственно) при отстройке ш, ФCO(ω) - спектральная плотность собственного фазового шума управляемого генератора (на частоте fout соответственно) при отстройке ω. Тогда, обозначив через Фout(ω) спектральную плотность фазового шума выходного сигнала, запишем
Т.е. спектральная плотность фазового шума выходного сигнала при заданной отстройке не может быть меньше наименьшего значения спектральной плотности фазового шума управляемого генератора и опорного синала при идеальном умножении частоты.
Следует так же отметить, что данное выражение вовсе не означает, что нельзя уменьшить мощность фазового шума, т.е. его интегральную характеристику. Как правило, при малых отстройках фазовый шум опорного генератора, пересчитанный на выходую частоту, меньше шума управляемого генератора и наоборот. Следовательно, имея управляемый генератор с низким уровнем шумов, уменьшив полосу передачи по фазе синтезатора, можно добиться уменьшения суммарной мощности фазового шума по отношению к идеальному умножению опорной частоты. Более того, этим часто пользуются при восстановлении частоты в системах связи. Если бы это было не так, то системы синхронной иерархии (SDH) давно бы рухнули, выйдя из синхронизма, поскольку частота каждого последующего передатчика восстанавливается из предыдущего.
6Вопрос о пределах интегрирования подробно изложен в предыдущих работах
Требуется разработать такую архитектуру синтезатора частот, которая бы обеспечивала минимальный уровень фазового шума на выходе. Задача минимизации фазового шума может быть решена различными способами в зависимости от поставленных требований, особенно тех, что определяют архитектуру. В связи с этим примем следующее:
Как будет показано ниже, синтезаторы целочисленного типа являются оптимальным выбором для мнимизации фазового шума при указанных требованиях. Поэтому этот тип взят за основу предлагаемого метода.
7Связь с максимальной частотой, генерируемой DDS в данном случае является следствием методов построения гибридных схем, обеспечивающих высокое разрешения по частоте за счет использования DDS совместно с синтезаторами целочисленного типа
3.1 Архитектура
На рисунке 1 показана структурная схема синтезатора целочисленного типа.
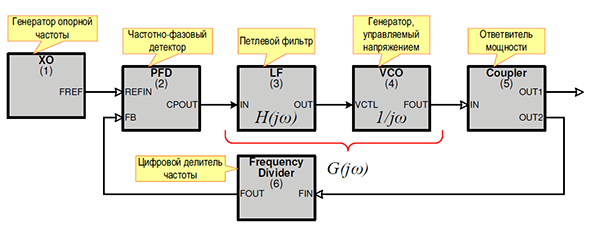
Рис. 1: Структурная схема синтезатора целочисленного типа
Он состоит из следующих блоков:
XO (1) - генератор опорной частоты (crystal oscillator);
PFD (2) - фазочастотный детектор (Phase Frequency Detector);
LF (3) - петлевой фильтр (Loop Filter);
VCO (4) - генератор, управляемый напряжением, ГУН, (Voltage Controlled Oscillator);
Coupler (5) - ответвитель мощности;
Frequency Divider (6) - делитель частоты.
Генератор опорной частоты выдает сигнал, подаваемый на положительный вход фазового детектора. На отрицательный вход фазового детектора подается сигнал отрицательной обратной связи. Разность фаз между опорным синлалом и сигналом обратной связи с выхода фазового детектора подается в виде сигнала (тока или напряжения) на петлевой фильтр, который обеспечивает необходимую фильтрацию и определяет частотную полосу передачи по фазе. Далее с петлевого фильтра сигнал подается на генератор, управляемый напряжением, далее - на ответвитель. Ответвитель обеспечивает согласованное разделение сигнала на два выхода, один из них, обладающий большей мощностью, является выходом системы, другой подается на цифровой делитель частоты, который, собственно и замыкает петлю обратной связи.
На рисунке 2 изображена эквивалентная статическая зависимость выходного сигнала фазового детектора от разности фаз входных сигналов. По вертикальной оси отложено напряжение или ток, в зависимости от типа выхода детектора. Т.е. передаточную характеристику фазового детектора можно представить следующим образом:
Рис. 2: Зависимость выходного сигнала фазового детектора от разности фаз входных сигналов
Рис. 3: Принцип действия фазового детектора
Поскольку зависимость не периодическая и не меняет знака при |Δφ| > 2π, как например, в детекторе, построенном на смесителе8, то он является не только фазовым, но и частотным детектором, именно в этом и заключается возможность захвата в широком диапазоне, что позволяет создать октавный синтезатор. Принцип действия детектора представлен на рисунке 3. Он представляет собой автомат, имеющий пять9 состояний (-2, -1, 0, +1, +2), переключаемый по переднему фронту опорного сигнала (REFIN) и сигнала обратной связи (FB). Сигнал REFIN прибавляет к состоянию единицу, а сигнал FB наоборот, вычитает. Состояниям -2 и -1 соответствует —V0 на выходе CPOUT, 0 - 0, +1 и +2 — +V0.
8Имеется ввиду умножитель двух сигналов (mixer)
9В более простом случае состояний может быть три. При этом линейная область остается прежней, немного увеличится время захвата частоты
Передаточная характеристика ГУНа определяется следующим образом. Приняв зависимость частоты на выходе от управляющего напряжения линейной [2], запишем:
Поскольку частота является производной фазы по времени, то
тогда передаточная характеристика генератора, управляемого напряжением в частотной области будет
Для упрощения записи объединим передаточные характеристики детектора V0/4π, петлевого фильтра H(jω), ГУНа KVCO/jω:
Делитель частоты представляет собой цифровой счетчик по модулю N, его передаточная характеристика по фазе равна соответственно 1/N. Уравнение для замкнутой петли обратной связи имеет таким образом вид:
где φref - фаза опорного сигнала, φout - фаза выходного сигнала. Выразив φoutref, запишем
Следует отметить, что G(jω) имеет полюсы в нуле, и |G(jω)| → ∞ при ω → 0. С другой стороны |G(jω)| → 0 при ω → ∞. Таким образом, как и следовало ожидать, в нуле коэффициент передачи по фазе точно равен N, - для этого, собственно, и нужен синтезатор, а на высоких частотах (т.е. при больших отстройках) обращается в ноль.
Следует отметить, что в приведенных выше выражениях мы имели дело не самими генерируемыми сигналами, а с их фазами, как функциями времени, причем в частотной области.
3.2 Анализ источников фазового шума
Для дальнейшего анализа источников шума рассмотрим математическую модель, изображенную на рисунке 4. Модель включает в себя следующие источники10:
φref - фазовый шум опорного генератора;
φPFD - суммарный фазовый шум фазо-частотного детектора и делителя частоты;
φVCO - фазовый шум генератора, управляемого напряжением [5];
φout - фазовый шум на выходе системы.
10Данная модель не включает собственный шум петлевого фильтра, поскольку при корректном подборе параметров и элементов (операционного усилителя, конденсаторов) его влиянием можно пренебречь [3]
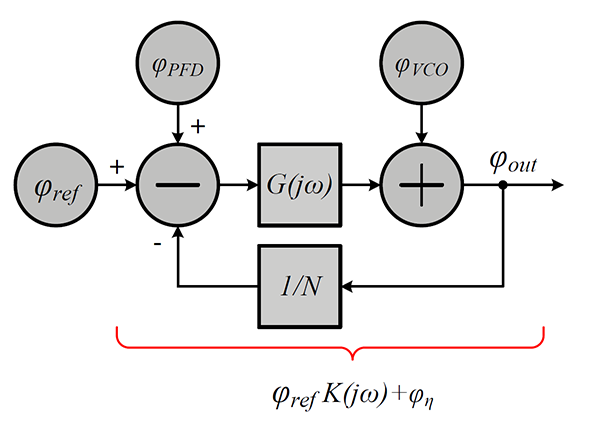
Рис. 4: Математическая модель синтезатора целочисленного типа
Следуя модели, выпишем уравнение, связывающие перечисленные выше параметры.
Выразив φout через входные параметры, найдем передаточные характеристики для каждого из них.
Из данного выражения следует, что передаточная характеристика для φref и φPFD представляет собой фильтр низких частот (ФНЧ) с коэффициентом усиления N на нулевой частоте, а для φVCO - фильтр высоких частот (ФВЧ), как показано на рисунке 5. Следует также отметить, что частоты срезов для данных ФНЧ и ФВЧ совпадают. На данном рисунке также отображены спектральные плотности средней мощности соответствующих случайных процессов (шумов).
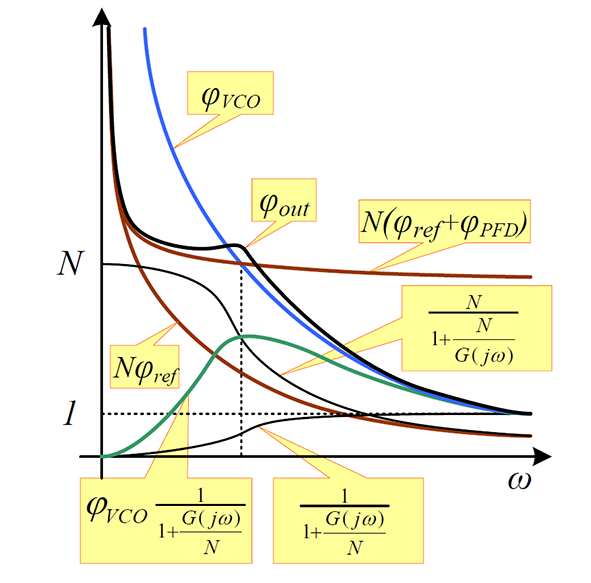
Рис. 5: Передаточные характеристики синтезатора
Для выбора оптимальных с точки зрения минимизации интегрального фазового шума на выходе системы параметров, рассмотрим зависимости спектральной плотности мощности источников шума от частоты. Спектральная плотность фазового шума опорного генератора достаточно мала при небольших отстройках. При больших отстройках, с учетом умножения на N (т.е. N2 по мощности) она становится существенной по отношению к шуму ГУНа при той же отстройке. Шум фазового детектора имеет достаточно пологую характеристику и превалирует над шумом опорного генератора, начиная с малых частот. Как показано на рисунке 5, существует точка пересечения кривой шума ГУНа и суммарного шума опорного генератора и фазового детектора. Очевидно, что для минимизации интегрального шума на выходе следует подобрать петлевой фильтр так, чтобы его частота среза находилась в данной точке. Таким образом, в области, где шум ГУНа больше (т.е. при малых отстройках), он подавляется эквивалентным ФВЧ, а там, где больше шум фазового детектора, он подавляется, соответственно, эквивалентным ФНЧ.
Следует отметить, что спектральная плотность шума фазового детектора убывает с ростом частоты сравнения пропорционально N (т.е. √N по амплитуде). Это означает, что целесообразнее подавать более высокую опорную частоту. С другой стороны с ростом частоты сравнения увеличивается и минимальный шаг перестройки.
Несмотря на развитие элементной базы, шум суммарный детектора и делителя остается на несколько порядков выше шума опорного генератора. С другой стороны, мы не можем заменить фазовый детектор другим элементом, например, смесителем, поскольку невозможен будет стабильный захват в широком диапазоне частот. Следовательно, для дальнейшего улучшения характеристик, необходимо каким-нибудь образом скомпенсировать их влияние. Этому и посвящены дальнейшие разделы.
3.3 Преимущества и недостатки
Поскольку в состав синтезатора так или иначе входят такие элементы, как опорный генератор, фазовый детектор и делитель частоты, то результирующие характеристики в плане фазового шума ими во многом определяются. Наилучшим из сигналов опорной частоты является тот, что взят непосредственно с опорного генератора, т.е. фиксированной частоты. Ни один элемент DDS не сравнится с этими характеристиками. Среди делителей, включая тот же DDS, лучшим по характеристикам фазового шума и чистоте гармонических составляющих SFDR (Spurios Free Dinamic Range) является целочисленный делитель. Поэтому оптимальным вариантом (при указанных выше требованиях) для минимизации фазового шума оказывается целочисленный синтезатор. Есть, однако, у него существенные минусы - большой шаг перестройки. В связи с этим используются гибридные схемы [4, 1] на основе целочисленных синтезаторов, которые позволяют устранить и этот недостаток. Следует еще раз отметить, что ядром таких схем является целочисленный синтезатор, и его качественное построение является существенным шагом на пути создания таких систем.
Из рисунка 4 ясно, что шум фазового детектора и шум делителя входят в состав выражения 2 с тем же множителем, что и шум сигнала опорной частоты. существующее состояние элементной базы таково, что самые лучшие из этих элементов обладают характеристиками на один-два порядка хуже, чем качественный кварцевый опорный генератор. В связи с этим возникает вопрос, нельзя ли каким-либо образом устранить их влияние. Следующие разделы и посвящены этой теме.
4.1 Принципы и реализация
Предлагаемая реализация компенсации фазового шума основана на использовании такого элемента, как генератор гармоник (Comb Generator), обладающего характеристиками, сравнимыми с самим опорным генератором. Принцип работы такого генератора заключается в следующем. На вход подается качественный опорный сигнал со сравнительно низкой частотой, например, 100 MHz. На выходе генератор гармоник имеет очень короткие импульсы (порядка пикосекунд) с достаточно большой амплитудой (порядка вольт), следующие друг за другом с периодом, соответствующим частоте входного сигнала. Таким образом, в частотной области такой сигнал представляет собой набор дельта-функций одинаковой амплитуды, размещенных по оси частот с периодом, равным частоте входного сигнала. Современные генераторы гармоник позволяют получить гармоники с неравномер-ностью менее 10 dB в полосе до 20 GHz! При этом качество, относительно существующих опорных генераторов, практически соответствует идеальному умножителю! Таким образом, с помощью данного генератора можно сформировать качественную гармонику на высокой частоте, относительно которой можно производить сравнение. Конечно, сигнал с выхода генератора гармоник нельзя подать на цифровой фазовый детектор, так же, как и невозможно отфильтровать требуемую гармонику, однако, если сравниваемые частоты близки или, тем более, одинаковы, то в качестве фазового детектора можно воспользоваться смесителем. В качестве управляемого элемента вместо ГУНа можно воспользоваться фазовращателем, управляемым напряжением. Современные фазовращатели позволяют сдвигать сигнал от 0 до 720° при более чем октавном частотном диапазоне.
4.2 Архитектура
На рисунке 6 изображена архитектура целочисленного синтезатора с предложенным методом компенсации фазовых шумов детектора, делителя и ГУНа. Она состоит из обычной петли автоподстройки частоты и фазы и дополнительной петли компенсации.
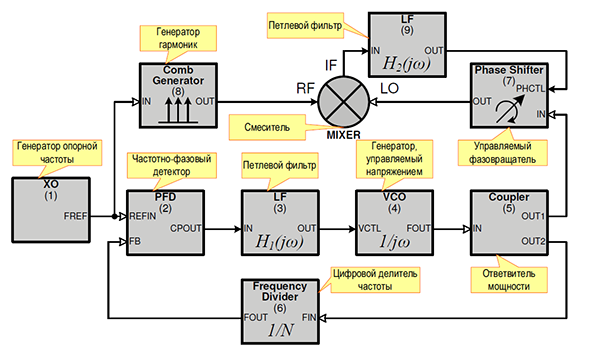
Рис. 6: Структурная схема синтезатора с компенсацией фазового шума
На рисунке изображено следующее:
XO (1) - генератор опорной частоты (crystal oscillator);
PFD (2) - фазочастотный детектор (Phase Frequency Detector);
LF (3) - петлевой фильтр (Loop Filter);
VCO (4) - генератор, управляемый напряжением, ГУН, (Voltage Controlled Oscillator);
Coupler (5) - ответвитель мощности;
Frequency Divider (6) - делитель частоты;
Phase Shifter (7) - фазо-сдвигатель, управляемый напряжением;
Comb Generator (8) - генератор гармоник (Comb-генератор);
LF (9) - петлевой фильтр (петли компенсации);
Mixer - смеситель.
Первая петля генерирует сигнал требуемой частоты, фазу которого можно представить следующим образом (рис. 4):
где
φL1out - фаза на выходе первой петли (Loop 1), К(jω) - коэффициент передачи замкнутой петли, G(jω) - коэффициент передачи разомкнутой петли, φη - суммарный фазовый шум первой петли, который требуется устранить. Фазу N-ой гармоники на выходе Comb-генератора можно выразить следующим образом:
Поскольку частота N-ой гармоники на выходе Comb-генератора и выходе первой петли точно совпадают, то на выходе смесителя, который играет роль фазового детектора, получим сигнал пропорциональный разности фаз φCombN и φL1out. Если считать опорный генератор близким к идеальному, то его фазу можно представить, как
следовательно в частотной области
где δ'(ω) - первая производная дельта-функции Дирака. Таким образом, разность выражений (5) и (3) равна φη, т.к. К(jω) = N при ω = 0. Далее сигнал ошибки, пропорциональный φη с выхода смесителя подается на петлевой фильтр с передаточной характеристикой H2(jω) и далее на управляющий вход фазо-сдвигателя, таким образом замыкая вторую петлю обратной связи.
4.3 Анализ предложенного подхода
На рисунке 7 изображена математическая модель, соответствующая предложенной архитектуре (рис. 6). Рассмотрим передаточную характеристику по фазе и преобразование шумовой составляющей с учетом второй петли.
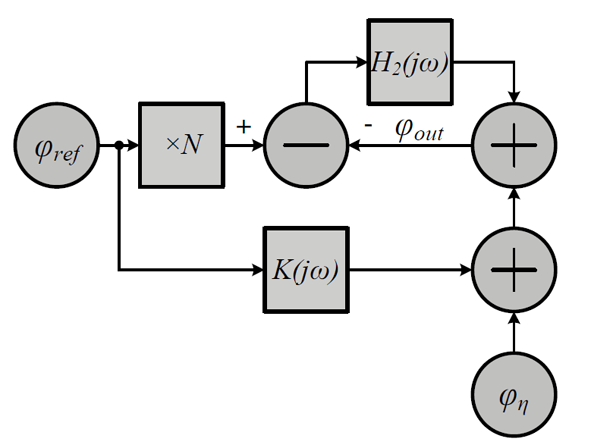
Связь рассматриваемых параметров, следуя рисунку, определяется следующим выражением
тогда выразив φout через входные параметры, получим
где φout - фаза на выходе синтезатора с учетом компенсации, φref - фаза сигнала опорного генератора, φη - суммарная шумовая составляющая на выходе первой петли, определенная выражением (4), K(jω) - передаточная характеристика первой петли относительно φref. Рассмотрим выражение (6) более подробно. Множитель при φref состоит из двух частей
Если частота среза ФВЧ, соответствующего передаточной характеристике 1/(1+H2(jω)) больше, чем эквивалентного ФНЧ K(jω), то первая часть множителя существенной роли не играет и может быть опущена при дальнейшем рассмотрении. Вторая часть представляет собой фильтр ФНЧ с коэффициентом N в нуле частот. Множитель при φη соответствует, как уже было отмечено фильтру высоких частот.
На рисунке 8 изображены соответствующие передаточные характеристики и спектральные плотности фазы, поясняющие влияние второй петли.
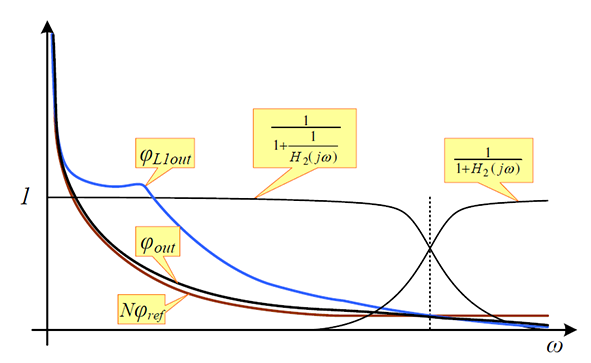
Рис. 8: Передаточные характеристики синтезатора с компенсацией
Таким образом при прохождении через всю систему фаза опорного сигнала умножается на N без каких-либо искажений вплоть до частоты среза второй петли, а на более высоких частотах подавляется. В то время, как суммарный шум от всех источников, входящих в первую петлю, подавляется до частоты среза. В этом и заключается эффект компенсации шума.
Из приведенного выше также следует, что частоту среза второй петли целесообразно выбирать в точке пересечения кривой спектральной плотности фазового шума первой петли и шума опорного генератора, умноженного на N (N2 по мощности). Таким образом, обеспечивается минимум интегральной мощности фазового шума. Принимая во внимание характеристики существующих на данный момент comb-генераторов, можно сказать, что предложенный метод компенсации позволит вплотную приблизиться к границе, определенной выражением (1).
В заключение просуммируем, что было сделано в приведенных выше разделах.
1. Рассмотрено назначение и область применения синтезаторов частот.
2. Приведена система основных параметров, определяющих архитектуру.
3. Указана нижняя теоретическая граница спектральной плотности средней мощности фазового шума для синтеза частот.
4. Поставлена задача минимизации фазового шума при указанных ограничениях.
5. Обоснован выбор и произведен анализ синтезаторов целочисленного типа, лежащий в основе предлагаемого метода.
6. Предложен и проанализирован метод компенсации фазового шума в цифровых синтезаторах частот, позволяющий получить характеристики, приближающиеся к теоретическому пределу.
Следует отметить, что проведенная работа является первым шагом на пути создания синтезатора с такими характеристиками. Здесь остались не рассмотренными технические аспекты построения устройства. Эти вопросы являются темами дальнейших работ, посвященных построению цифровых синтезаторов частот.
[1] Vsevolod Tanygin, “A Practical Design of a Low Phase Noise Airborne X- Band Frequency Synthesizer”, Microwave Journal, Vol. 49, No. 10, October 2006, pp. 92-114.
[2] M. Seo, J.Y. Lee and K.K. Lee, “A Varactor-tuned Oscillator with Linear Tuning Characteristic”, Microwave Journal, Vol. 45, No. 2, February 2002, pp. 100-114.
[3] W.O. Keese, “An Analysis and Performance Evaluation of a Passive Filter Design Technique for Charge Pump Phase-locked Loops”, National Semiconductor Application Note 1001, May 1996.
[4] D. Crook, “Hibrid Synthesizer Tutorial”, Microwave Journal, Vol. 46, No. 2, February 2003, pp. 20-38.
[5] D. Colin, “Externaly Induced VCO Phase Noise”, Microwave Journal, Vol. 45, No. 2, February 2002, pp. 20-41.
[6] W.F. Graves, “Managing Noise and Spurios within Complex Microwave Assemblies”, RF Design, No. 7, July 2003, pp. 26-36.