Для ознакомления с полноценным материалом, согласитесь и скачайте:
Статья в формате pdfВ работе представлена оценка спектральной плотности фазового шума на выходе цифрового делителя, входящего в состав синтезаторов частот, при воздействии аддитивного шума на опорный периодический сигнал на его входе. Проведен анализ преобразования аддитивного шума в фазовый на выходе делителя и его спектральных составляющих при входных воздействиях, находящихся в частотном диапазоне гораздо выше частоты сравнения фазового детектора.
Результатом анализа является методика оценки спектральных характеристик фазового шума на выходе делителя и характеристик выходного сигнала синтезатора частот. Разработаны рекомендации по проектированию подобных систем и методика их отладки, что представляет практический интерес для инженеров, занимающихся высокочастотной аналоговой техникой.
Построение современных средств цифровой радиосвязи, радиолокации, измерительного оборудования немыслимо без использования синтезатора частот. От качества генерируемого синтезатором сигнала во многом зависят характеристики и возможности всей системы, и в ряде случаев именно он является ограничивающим фактором, особенно на частотах выше 2-3 GHz, когда работа с сигналом требует особых приемов и материалов, свойственных СВЧ технике. Ниже речь будет об эффектах, имеющих место при высокочастотном цифровом синтезе, хотя аналогичные методы можно применить и для низкочастотной области.
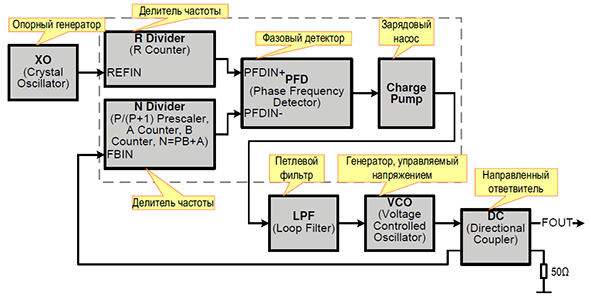
В состав практически любого синтезатора наряду с такими элементами, как ГУН (VCO), фазовый детектор (Phase Detector), зарядовый насос (Charge Pump), петлевой фильтр (Loop Filter) и направленный ответвитель (Directional Coupler), входит цифровой делитель частоты (Frequency Divider, Prescaler), рисунок 1. Каждый из этих элементов вносит свой вклад в результирующий фазовый шум на выходе синтезатора.

Рис. 1: Схема синтезатора частоты
Общепринятая оценка шума на выходе такой системы складывается из влияния опорного генератора, фазового детектора, петлевого фильтра и ГУНа. Математические выражения, связывающие эти параметры, методика расчета и измерения довольно подробно описаны в литературе по данной тематике [1, 3]. Влиянием делителей в большинстве случаев пренебрегают, поскольку сами по себе они не вносят существенных искажений, их собственный шум по отношению к опорному сигналу низок, а передаточная характеристика по фазе линейна. Однако не стоит забывать, что в реальных системах помимо собственных источников шума компонентов синтезатора, существуют внешние источники излучения, которые способны существенным образом повлиять на конечный результат.
Высокочастотные наводки на петлевой фильтр сказываются слабо, поскольку выход зарядового насоса и вход ГУНа, как правило, шунтированы керамическими конденсаторами. Связи между блоками, обведенными на рисунке 1 пунктирной линией, достаточно малы, т.к. обычно размещены в одном корпусе микросхемы, и практически не образуют контуров и, соответственно, менее подвержены внешнему излучению. Таким образом, наиболее подверженными в данном отношении участками являются связи между опорным генератором и входным делителем опорной частоты и между направленным ответвителем и входом делителя сравниваемой частоты, поскольку передаточная характеристика по фазе от этих точек до выхода пропорциональна коэффициенту N/R (порядка нескольких сотен) в области пропускания петлевого фильтра.
Аддитивный шум, наведенный на вход опорной частоты, после прохождения через цифровой делитель преобразуется в фазовый шум, дальнейший анализ которого производится известными методами [2]. Темой же данной работы является анализ преобразования аддитивного шума в фазовый на выходе делителя и его спектральных составляющих при входных воздействиях, находящихся в частотном диапазоне гораздо выше частоты сравнения фазового детектора. Результатом анализа является методика оценки спектральных характеристик фазового шума на выходе делителя и методы борьбы с такого рода эффектами.
Рассмотрим модель, показанную на рисунке 2. В нее входит опорный генератор детерминированного периодического сигнала s(t), генератор шума, представленного в виде случайного процесса f (t), сумматора, компаратора и цифрового делителя.
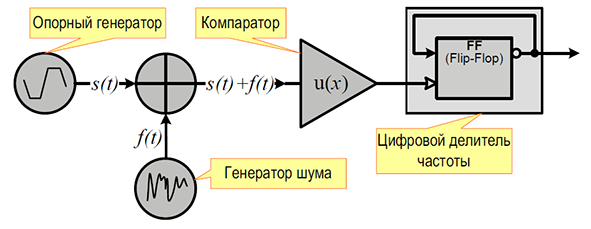
Рис. 2: Модель преобразования аддитивного шума в фазовый
Генератор шума и сумматор соответствуют модели аддитивного шума, наведенного на линию связи между генератором опорной частоты и входом делителя частоты в микросхеме цифрового фазового детектора (рис. 1). Компаратор представляет входной каскад делителя частоты в этой микросхеме, он сравнивает входной сигнал с нулем и выдает логический сигнал “0”, - если сигнал на входе меньше нуля и “1”, если больше либо равен нулю, т.е. компаратору можно сопоставить единичную функцию Уолша. В качестве цифрового делителя частоты приведен делитель на два. Фактически он состоит из двухтактного триггера, работающего по фроту (flip-flop), с инвертированным выходом, замкнутым на его вход.
Опорный генератор выдает синал s(t) с периодом Ts и конечной скоростью нарастания фронта в точке пересечения с нулем. Таким образом, если исключить шум, то на выходе компаратора будем иметь периодический сигнал с фронтами (моментами переключения из “0” в “1”), расположенными во времени строго через интервалы Ts. Если добавить шум (подразумевается, что уровень шума гораздо ниже уровня опорного сигнала), то моменты времени, в которые функция s(t) + f (t) проходит через ноль сместятся относительно своих номинальных точек. Эти смещения с учетом прохождения через делитель частоты и есть тот фазовый шум, который следует рассмотреть.
Для облегчения анализа разобьем задачу на следующие этапы:
2.1 Спектральные характеристики фазового шума, как непрерывного процесса во времени
2.1.1 Аналитическая оценка
Для определения непрерывного во времени смещения представим, что фронт сигнала s(t) может непрерывно двигаться по оси времени, и рассмотрим одну из реализаций случайного процесса f (t), рис. 3.
Рис. 3: Графическое представление фазового сдвига
На рисунке s(t) пересекает ноль в точке ts - это положение фронта в идеальном случае. В случае с шумом положение будет определяться пересечением s(t) и —f (t). Сдвиг будет равен разности точки пересечения и ts. Этот сдвиг, как функцию параметра ts, назовем т(ts), он является реализацией исследуемого случайного процесса.
Сделаем следующие предположения об опорном сигнале s(t) и шуме f(t):
1. процесс f(t) ограничен, т.е. ∃fmin, fmax < ∞ : fmin < f(m)(t) < fmax, ∀ m, t, где f(m)(t) - m-тая реализация процесса f (t) и E(f(m)(t)) = 0, где f(m)(t) - m-тая реализация процесса f(t), E[] - оператор усреднения по всем реализациям;
2. функция s(t) дифференцируема и ∀ε ∈ [min(f(t));max(f(t))], ∀t, ts ∈ R выполняется условие:
3. процесс f (t) стационарен в широком смысле, т.е. для функции плотности вероятности выполнены условия:
и
4. процесс f (t) дифференцируем в среднеквадратическом, т.е.
где f(m)(t) - m-тая реализация процесса f(t), E[] - оператор усреднения по всем реализациям;
5.∀ε ∈ [min(f(t));max(f(t))], ∀t, ts ∈ R выполняется условие:
В условии 1 требование на равенство нулю среднего значения не является существенным ограничением, поскольку это всего лишь приводит к постоянному сдвигу по фазе и, соответственно, может быть приведено к процессу с нулевым средним путем пересчета рабочей точки пересечения фронта.
Условие 2 означает линейность участка фронта опорного сигнала в области точки пересечения с нулем. В реальных устройствах при отсутствии серьезных ошибок при проектировании это всегда выполняется, поскольку существует ограничение на немонотонность опорного сигнала в области границ переключения.
Условия 3 и 4 являются обычными при использовании корреляционного подхода. Большинство реальных процессов, встречающихся в цифровой связи им удовлетворяют.
Условие 5 означает отсутствие двойных переключений и возможность интерполяции реализации процесса f (t) в области точки ts. Вообще, знак “много больше” в условии 5 служит лишь для большей точности оценки. Для сходимости результата вполне достаточно знака “больше”. Очевидно, что если это условие не будет выполняться, возникнут двойные переключения, что совершенно не приемлемо для физических систем, и рассматривать это вообще не стоит.
При практическом использовании для большинства встречающихся сигналов эти условия можно заменить одним: уровень опорного сигнала должен быть гораздо выше уровня шума.
Учтя приведенные выше ограничения, найдем связь между реализацией f(t) и реализацией τ(t). Обозначив s'(ts) через Ks, и воспользовавшись выражением (1), напишем:
Разложив реализацию f(t) в степенной ряд до первого члена в точке ts, с учетом выражения (2), получим:
В виду малости производной реализации f(t) по отношению к Ks разложим знаменатель в ряд до первой степени:
Выражение (4) будем в дальнейшем использовать для нахождения спектральных характеристик процесса τ(ts). Для этого определим спектральную плотность средней мощности и выразим ее через оператор усреднения по реализациям во временной области. Поскольку в выражение (4) входит производная, то свяжем усреднение по реализациям производных с производными от усредненного значения.
И так, пусть имеется m-тая реализация f(m)(t) случайного процесса f (t). Обозначим через f(m)T(t) функцию
где E() - оператор усреднения по реализациям. Перейдем в выражении (5) к временной области.
тогда
где
Определив таким образом корелляционную функцию B(t), мы несколько расширили класс рассматриваемых процессов. Если в выражении (4) пренебречь вторым слагаемым, то воспользовавшись выражением (7), найдем спектральную плотность средней мощности процесса r(ts):
Выражение (9) дает приближение первого порядка, составляющие фазового шума соответствуют той же области частот, что и у аддитивного шума на входе. Для нахождения других спектральных составляющих постараемся учесть второе слагаемое. Подставив выражение (4) в (8) получим
Подставим получившееся выражение в (7) и представим результат в виде
где
Первому слагаемому при подстановке в (6) и с учетом стационарности в широком смысле процесса f(t) соответствует результат (9). Если предположить, что производная процесса слабо коррелирована с его значением в этой точке, то усреднение от произведения равно произведению средних значений. Но так как среднее от производной равно нулю, то второе и третье слагаемое так же равно нулю. Таким образом, четвертое слагаемое можно записать в виде
Поскольку процесс f (t) является стационарным в широком смысле, то входящие в интеграл выражения не зависят от переменной интегрирования t и можно записать
где
Выразим корреляционную функцию производной Bf'(ts) через корреляционную функцию самого процесса f(t) - Bf(ts).
Т.к. из сходимости в среднеквадратическом следует сходимость по вероятности, то
учтя выражение (8), запишем
Поскольку для стационарного в широком смысле процесса
то
Таким образом, получим корреляционную функцию процесса τ(ts)
Подставив ее в выражение (6), и приняв во внимание, что оператор дифференцирования во временной области соответствует умножению на jω, а умножение - свертке в частотной, получим
Это и есть искомое выражение, учитывающее спектральные составляющие второго порядка.
2.1.2 Об области применения оценки
При переходе от выражения (10) к (11) мы воспользовались предположением, что процессы f(t) и f'(t) слабо связаны друг с другом, в результате чего сократилось 2-е и 3-е слагаемое в выражении (10), а четвертое представилось в виде произведения двух усреднений. Вообще говоря, это довольно жесткое требование, в частности не выполнимое для детерминированных сигналов. Однако, если принять во внимание предел интегрального соотношения в выражениях Вτ2(ts), Bτ3(ts) и Bτ4(ts), то мы придем к тем же результатам упрощения общего выражения для более широкого класса процессов.
Рассмотрим случай детерминированного гармонического воздействия f(t) = sin(t). Тогда произведению f(t)f(t — ts)f'(t) будет соответствовать сумма гармонических составляющих с фазами t — ts, 3t — ts, t+ts, интеграл по t будет конечным, а предел, входящий в состав выражения Вτ2(ts) будет равен нулю. То же самое относится и к Вτ3(ts). Результат 4-го слагаемого в выражении (10), очевидно, корректен, поскольку средним от детерминированной функции является само значение функции. Таким образом, выражение (12) вполне применимо и для детерминированного гармонического воздействия. Единственным существенным ограничением остается слабая версия условия 5 (со знаком “больше”), - скорость нарастания фронта должна быть больше максимальной производной наведенной синусоиды.
2.1.3 Анализ фазового сдвига при гармоническом воздействии
Поскольку при отладке и тестировании наиболее распространенными являются синусоидальные воздействия, то рассмотрим их более подробно.
Спектральная плотность мощности синусоиды с частотой ωf равна
Подставив это выражение в (12), получим
На рисунке 4 отображены приведенные графики численного решения уравнения (3) для воздействия
а так же уравнение — sin(t), являющееся ассимптотой при ωf→0.
Рис. 4: Приведенные решения уравнения для гармонического воздействия разной частоты
Как видно из графика при увеличении частоты и приближении к границе условия 5 сильнее сказывается нелинейность уравнения (3). На рисунке 5 представлена зависимость уровня первой, второй и третьей гармоники решения τ(ts) от частоты гармонического входного воздействия ωf.
Рис. 5: Уровень 1-ой, 2-ой и 3-й гармоники от частоты
Следует отметить, что уровень первой гармоники с ростом частоты практически остается без изменений, а уровень второй гармоники растет со скоростью 20dB/dec, что находится в согласии с полученным результатом (12).
На рисунке 6 показана крупным планом область нелинейности и соответствующая ошибка оценки. Таким образом, даже при достижении граничного условия по частоте, величина ошибки первой гармоники составляет около 1dB, а второй гармоники - не более 3dB.
Рис. 6: Ошибка оценки в нелинейной области
2.2 Фазовый шум, как дискретный во времени процесс
В предыдущем разделе мы рассмотрели фазовый шум, как непрерывный во времени процесс, образуемый за счет непрерывного сдвига фронта опорного сигнала по оси времени. Теперь зададимся вопросом, как изменятся спектральные характеристики процесса, если фронт опорного сигнала появляется последовательно через равные промежутки времени, что и имеет место в реальном устройстве.
Пусть период опорного сигнала равен T. Представим сдвиги в моменты времени kТ, k ∈ N в виде дельта-импульсов с амплитудой τ(kТ). Выразим спектр данной реализации через спектр τ(ts):
Воспользовавшись соотношением
получим
т.е. результирующий спектр равен сумме последовательно сдвинутого исходного спектра. Следует обратить внимание, что амплитуда τ1/T(jω) обратно пропорциональна периоду T. Если спектры не перекрывают друг друга, то для спектральной плотности мощности можно написать:
или в пересчете на фазу (φ=2πτ/T)
2.3 О спектральной плотности мощности периодического сигнала с фазовым шумом
Выражение (14) при малых φ соответствует величине соотношения первой гармоники сигнала на выходе компаратора к спектральной плотности шума при малой отстройке частоты. Эта величина выражается в едниницах dBc/Hz (децибел относительно несущей на герц) для заданной отстройки и является основной характеристикой качества сигнала гетеродина. Ее легко измерить при помощи анализатора спектра с достаточно узкополосным радиофильтром (RBW). Т.е. у периодического сигнала, подверженного фазовым шумом его спектральная плотность мощности вблизи основной гармоники в точности повторяет спектральную плотность средней мощности фазового шума Фφ(ω). Это легко показать на примере синусоидального сигнала s(t) = sin(ωst) и малого фазового сдвига φ(t). Результат воздействия фазового шума в таком случае будет
Разложив sin(φ(t)) и cos(φ(t)) в виду малости φ(t) в ряд до первой степени, получим:
Таким образом, спектральной плотностью мощности рассматриваемого сигнала, подверженного действию фазового шума, является дельта-функция, соответствующая исходному опорному сигналу s(t) и смещенная на ωs спектральная плотность средней мощности процесса φ(t). Этот факт дает возможность экспериментально определять спектральные характеристики фазового шума с достаточно высокой точностью.
2.4 Влияние цифрового делителя частоты
Для дальнейшего рассмотрения процесса преобразования фазового шума следует отметить, что подавляющее большинство фазовых детекторов, входящих в состав микросхем PLL (Phase Lock Loop), работают по одному из фронтов сигнала, для определенности скажем, переднему. Поэтому значение сдвига важно лишь для этого фронта, положение другого практически никакого влияния не оказывает.
Рассмотрим теперь целочисленный делитель. По сути, он представляет собой счетчик по модулю N, где N и есть коэффициент деления. Переключение счетчика так же происходит по одному из фронтов сигнала, подаваемого на вход синхронизации. Таким образом, фазовый сдвиг на том фронте, по которому происходит переключение, без изменений транслируется на выход делителя (рис. 7) плюс к нему добавляется постоянное значение задержки. Очевидно, что эта постоянная составляющая дополнительного шума не вносит, поэтому ее можно не учитывать.
Рис. 7: Преобразование фазового шума на делителе частоты
Таким образом, значение сдвига τ(kТ), где T - период сигнала на входе, при прохождении через делитель не меняется, но сами сдвиги появляются в N раз реже. Фактически это эквивалентно увеличению периода T в N раз. Поэтому для нового значения периода сигнала на выходе делителя запишем:
Подставив это выражение в (13), получим
Это означает, что мощность фазового шума в выделенной полосе уменьшается в N2 раз, а наложение спектра происходит периодом по частоте в N раз меньше. Другими словами в N раз уменьшается частота дискретизации процесса τ(ts).
2.5 Результирующее выражение для оценки фазового шума
Приняв во внимание выводы, сделанные в предыдущих разделах, выпишем результирующее выражение для расчета фазового шума на выходе цифрового делителя при аддитивном воздействии на опорный сигнал, подаваемый на его вход:
где Φf(ω) - спектральная плотность средней мощности входного аддитивного шума, Ks - скорость нарастания фронта тактового (опорного) сигнала на границе переключения входного каскада делителя, T - период опорного сигнала на входе делителя, N - коэффициент деления целочисленного цифрового делителя частоты.
3.1 Анализ характеристик выходного сигнала
В приведенных выше разделах был рассмотрен один из узлов цифрового синтезатора частот - целочисленный делитель. Для практического применения полученных результатов необходимо определить влияние исследуемого блока в рамках всей системы и выяснить зависимость основных характеристик выходного сигнала синтезатора от тех или иных параметров решаемой задачи. Для этого приведем ряд свойств, используемых в дальнейшем для анализа характеристик выходного сигнала.
Как известно, синтезатор частот представляет собой систему ФАПЧ, опрерирующую с фазами периодических сигналов, т.е. при расчете используют не сами сигналы на входе или выходе, а их фазы. Т.е. опорным воздействием (рис. 1) будет служить не сам сигнал s(t), а его фаза φs(t), соответственно для выхода - φout(t). Поскольку фазы так же являются функциями или процессами от времени, то им, как и сигналам, можно сопоставить изображения в частотной области φs(jω) и φout(jω). Синтезаторы частот, выполненные на основе цифрового фазового детектора, являются линейными системами, поэтому фазу выходного сигнала можно выразить через фазу входного следующим образом:
где Кφ(jω) - передаточная характеристика по фазе в частотной области.
Передаточная характеристика замкнутой петли ФАПЧ от входа REFIN до выхода FOUT (рис. 1) соответствует фильтру нижних частот с усилением на нулевой частоте N/Д точно, приблизительно столько же в полосе пропускания. Ширина полосы этого фильтра, неравномерность и скорость спада АЧХ зависят от параметров зарядового насоса (Charge Pump), петлевого фильтра и ГУНа. Ширину полосы нельзя сделать сколь угодно малой, поскольку чем меньше полоса, тем дольше время захвата, меньше устойчивость. Есть и еще один существенный момент - обычно у ГУН достаточно низкие шумы при высокой отстройке от генерируемой частоты, но высокие вблизи. Как будет показано ниже, в полосе пропускания по входу REFIN шумы ГУНа по входу FBIN наоборот подавляются. В связи с этим подбирают оптимальную полосу в плане минимизации интегральных характеристик фазового шума на выходе. Для октавных синтезаторов на частоту 1-2GHz при частоте сравнения фазового детектора около 2MHz оптимальная полоса передаточной характеристики получается около 10-100kHz.
Передаточная характеристика от входа FBIN до выхода FOUT соответствует тому же фильтру низких частот, но с усилением в полосе пропускания 1/1.
Для сигнала, подаваемого на вход REFIN можно написать
где ωs - частота опорного сигнала, φ(t) - фазовый шум на входе REFIN. Тогда в частотной области это выражение можно переписать в следующем виде:
где δ'(ω) - производная дельта-функции Дирака. Для сигнала на выходе, приняв во внимание коэффициент передачи на нулевой частоте, получим
Таким образом, средняя частота сигнала на выходе будет с точностью равна произведению (N/R)ωs, а фазовый шум на выходе будет определяться передаточной характеристикой Kφ(jω).
Шумы на выходе относительно входа FBIN будут определяться передаточной характеристикой, соответствующей упомянутому выше фильтру низких частот.
3.2 Рекомендации по проектированию
На основе проведенного анализа и практического опыта разработан ряд рекомендаций по устранению фазовых шумов, связанных с аддитивными составляющими в сигнале опорной частоты и сигнале обратной связи в цифровом синтезаторе частоты.
3.2.1 Экранирование
При размещении различных функциональных блоков в одном корпусе или тем более на одной плате добиться полного контроля над спектральными составляющими излучения, генерируемого различными сигналами, довольно сложно. Сигналы могут перекрываться в частотной области или находиться рядом друг с другом, так что их разделение путем фильтрации становится невозможным.
Одним из решений этой проблемы является повышение электромагнитной изоляции путем экранирования. Блоки, работающие на разных частотах, особенно не кратных друг другу и размещенных близко в частотной области, целесообразно располагать в отдельных секциях металлического корпуса.
Следует устранить длинные щели, образуемые в местах соединения с крышкой корпуса, а так же платы с нижней поверхностью стенки секции, если используется одна плата на несколько секций. Ослабление излучения резко увеличивается при разбиении длинной щели на несколько коротких по отношению к длине волны.
Под стенкой секции на плате следует предусмотреть двойной ряд металлизированных отверстий, соединенный с металлизированным слоем земли во внутренних и соответствующими полигонами на внешних слоях. Естественно, в месте соединения стенки секции с полигоном земли следует предусмотреть освобождение от маски. Эта мера является обязательной, поскольку существенная часть излучения располагается внутри платы. К тому же, поскольку диэлектрическая проницаемость материала платы больше единицы, то длина волны становится меньше, что еще более усугубляет ситуацию. Переходные отверстия, соединенные с металлизированными полигонами, образуют экран внутри платы.
Использование отдельных секций для каждого блока является дорогим решением в плане используемого пространства и материалов корпуса, и печатной платы. Поэтому в качестве изоляции можно использовать металлизированные полигоны, соединенные металлизированными отверстиями с плоскостью земли, как показано на рисунке 8.
Рис. 8: Экран, выполненный в виде металлизированных полигонов на печатной плате
В особых случаях, если стоит задача достичь максимальных характеристик, то блок синтезатора размещают на отдельной плате и, даже, в отдельном корпусе. При оптимизации по стоимости изделия синтезатор можно разместить и на общей плате, но рекомендуется выделить для него отдельную секцию или, по крайней мере, накрыть экраном из фольги.
Еще одним способом уменьшить наводки является использование дифференциальных линий. Это наиболее эффективно в случае двухслойной печатной платы, поскольку толщина платы в таком случае обычно получается больше минимального зазора между проводниками, и при использовании дифференциальных линий площадь эквивалентного контура получается меньше, соответственно меньше и уровень наведенного сигнала.
В любом случае в первую очередь следует обеспечть как можно большую изоляцию для опорного сигнала, поскольку, как было показано в предыдущих разделах, фазовый шум на этом входе имеет высокий коэффициент передачи к выходу, многократно усиливаясь. Затем, так же следует уделить внимание сигналу обратной связи.
3.2.2 Фильтрация
Одним из простых и доступных средств уменьшения влияния аддитивного шума является фильтрация. На рисунке 9 изображены два варианта построения тракта опорного сигнала, - для одиночного (single ended), рис. а, и дифференциального (differential-mode), рис. б, сигнала.
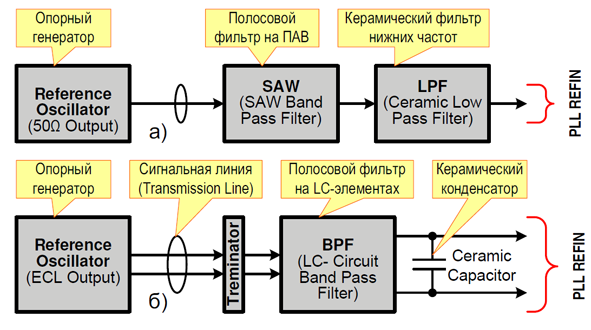
Рис. 9: Фильтрация опорного сигнала
В случае одиночного сигнала (single ended) тракт состоит из длинной линии, на которую наводится аддитивный шум, полосового фильтра на ПАВ и керамического фильтра. Фильтры следует размещать как можно ближе к входу REFIN микросхемы PLL и именно в указанной последовательности. Фильтр на ПАВ давит шум на нижних и средних частотах, керамический фильтр нижних частот давит верхние частоты, частично пропускаемые первым фильтром. При использовании ПАВ следует уделить внимание уровню сигнала на входе REFIN, поскольку ПАВ, расчитанный на низкие частоты имеет довольно высокие вносимые потери (insertion loss) - 10-15dB для частот около 100MHz. Если опорная частота мала, например, 10MHz, то фильтр ПАВ лучше заменить на LC-фильтр, в связи с тем, что ПАВ на низкие частоты не выпускается либо имеет очень высокие потери.
Полосовой фильтр предназначен для подавления не только наведенного сигнала, но и суб-гармоник, которые присутствуют в опорном сиганле, если опорный генератор работает не на основной гармонике. При использовании термостабилизированного генератора с малым разбросом частоты в заданном диапазоне температур, вместо фильтра на ПАВ можно использовать кварцевый фильтр. При этом следует обратить особое внимание на температурную стабильность используемых компонентов.
В случае дифференциального сигнала (differential-mode) строение тракта аналогично, за исключением дополнительных ограничений на элементную базу - фильтры ПАВ и керамические фильтры в дифференциальной форме, как правило, не выпускаются. Поэтому роль полосового фильтра играет обычный фильтр на дискретных LC-элементах, а керамического фильтра - высокочастотный конденсатор.
Следует отметить, что отфильтровать опорный сигнал достаточно просто по нескольким причинам. Во-первых, его частота мала по отношению к наведенному сигналу, лежащему обычно в гигагерцовом диапазоне. Шумы в низком и среднечастотном диапазоне в основном относятся к прохождению по цепям питания и устраняются за счет использования отдельного стабилизатора для генератора и микросхемы PLL, а так же дополнительного подавления полосовым фильтром. Во-вторых, частота опорного гене-ратора постоянна, что позволяет использовать узкополосные фильтры без динамической перестройки.
Иначе дело обстоит с сигналом обратной связи. Во-первых, его частота обычно лежит в том же диапазоне, что и потенциально наводимый сигнал. Во-вторых, частота меняется в заданном диапазоне. Даже в случае генерации постоянной частоты в нормальном режиме, в процессе захвата его частота меняется, и если поставить узкополосный фильтр на номинальную частоту, то захват частоты петлей ФАПЧ станет невозможным.
В связи с этим, фильтрация сигнала обратной связи мало эффективна. Единственно, что можно посоветовать, - использовать как можно более короткую линию. В случае, если наведенный сигнал лежит вне полосы, можно, конечно, использовать полосовой керамический фильтр с полосой, чуть больше полосы перестройки используемого ГУНа. К счастью, в отличие от опорного сигнала, шумы обратной связи сказываются на выход в меньшей степени.
3.2.3 Выбор частоты сравнения фазового детектора и промежуточной частоты тракта
На плате может присутствовать множество источников излучения. Это может быть как сигнал аналогового тракта, так и другой синтезатор (рис. 10).
Рис. 10: Возможные источники излучения
Воспользовавшись свойствами передаточной характеристики, в некоторых случаях можно свести к минимуму влияние наведенного шума за счет выбора частоты сравнения фазового детектора и промежуточной частоты тракта.
Синтезатор можно представить в виде цифрового фильтра с периодической характеристикой. Период в таком случае равен частоте сравнения фазового детектора. Максимальное подавление в таком случае достигается, если частота наведенного воздействия ωf равна
где ωPFD - частота сравнения фазового детектора
ωs - частота опорного сигнала. В таком случае, если ширина полосы наведенного сигнала меньше разности частоты сравнения фазового детектора и удвоенной граничной частоты пропускания, то он весь будет лежать в области подавления передаточной характеристики по фазе.
Рассмотрим еще один случай. Пусть наведенный сигнал является периодическим с низким уровнем шума, например, второй синтезатор, размещенный на той же плате. Тогда подобрав его частоту так, чтобы она была кратной частоте сравнения фазового детектора, мы получим на выходе постоянное смещение по фазе, которое не оказывает влияние на качество сигнала на выходе. Это можно сделать, подав опорный сигнал с одного и того же генератора, как показано на рисунке 10 и выбрав один и тот же коэффициент деления R.
3.3 Методика отладки
Процесс отладки состоит из последовательной проверки отдельных частей схемы и их влияния друг на друга. Ниже мы рассмотрим только те этапы, которые относятся к рассматриваемому вопросу. Подразумевается, что на этапе проектирования были сделаны необходимые расчеты по оценке ожидаемых характеристик. Ниже так же предполагается, что синтезатор приведен в работающее состояние, настроен петлевой фильтр, но качество сигнала оказалось неудовлетворительным.
Несмотря на то, что процесс отладки сложно представить в виде обобщенной формализованной методики, тем не менее можно выработать ряд следующих шагов по устранению типовых ошибок.
Включив питание, проверить качество (спектральный состав) и уровень опорного сигнала на выходе фильтров, сравнить с ожидаемым. Если уровень выше расчетного - следует подстроить аттенюатор, если ниже, то этому может быть несколько причин. Возможно, смещена полоса фильтров или плохо согласованы сопротивления элементов тракта опорного сигнала. Если спектральный состав вблизи основной гармоники не соответствует ожидаемому, - вероятно, это помехи по питанию - обеспечить надлежащую фильтрацию цепей питания. Если уровень субгармоник выше требуемого - увеличить подавление полосового фильтра. На практике спектральный состав опорного сигнала полностью можно исследовать только на низких и средних частотах (т.е. в узком диапазоне), т.к. это требует большого разрешения фильтра RBW анализатора спектра, поэтому отображение широкого диапазона частот занимает слишком много времени.
Убедившись в качестве опорного сигнала, переходим к проверке выходного сигнала. Если спектральный состав вблизи основной гармоники неудовлетворителен, проверить питание микросхемы синтезатора, ГУНа, петлевого фильтра (если он активный). Отстройка гармонических составляющих, так называемых “шпор” (spurs) от основной частоты на выходе синтезатора равна частоте помех по питанию. Таким образом, можно определить источник шума. Если дело не в питании, то следует рассчитать ряд возможных частот наведенного на вход REFIN высокочастотного сигнала и сравнить его с набором присутствующих на плате частот и, таким образом, определить источник наведенного излучения и точное значение частоты. С высоким разрешением радиофильтра (RBW) анализатора спектра проверить, действительно ли такой сигнал присутствует в спектре опорного сиганла. В ряде случаев видна вторая гармоника фазового сдвига, располо-женная чуть ниже первой, что указывает на заметную нелинейность преобразования аддитивного шума в фазовый. В результате, в соответствии с проведенным теоретическим анализом можно сделать вывод, что наведенный сигнал лежит на высокой частоте и имеет уровень, близкий к появлению двойных переключений. Пути решения - увеличить подавление фильтра высоких частот, а в следующей модификации печатной платы увеличить электромагнитную изоляцию, поместив источник в отдельную секцию или изменив топологию размещения элементов.
В приведенных выше этапах проверка производится в отсутствие сигнала в основном аналоговом тракте. Следующим шагом является проверка отсутствие наводок на опорный сигнал со стороны линейного тракта. В начале следует разбить входной частотный диапазон на несколько равных отрезков и рассчитать ближайшие к ним частоты, образующие небольшую отстройку от частоты, кратной частоте сравнения синтезатора. Отстройка должна быть меньше полосы пропускания передаточной характеристики по фазе, но большей, чем RBW. Подключить ко входу тракта источник гармонического сигнала максимального уровня и, переключая последовательно частоту по расчетным значениям, следить за спектральным составом сигнала на выходе вблизи основной гармоники. Если на расчетной отстройке появятся составляющие (шпоры), значит это сигнал наводится на вход опорной частоты. Еще одним признаком этого эффекта является квадратичная зависимость уровня составляющих от уровня подаваемого сигнала. Т.е. при уменьшении уровня сигнала на входе соотношение сигнала к шпорам увеличится во столько же раз (на столько же децибел). Это следует из того, что уровень аддитивной составляющей пропорционален сигналу в тракте, уровень фазового шума пропорционален аддитивной составляющей, далее при прохождении смесителя (рис. 10) фазовый шум сворачивается с тем же сигналом, образуя зависимость второй степени.
В заключение приведем основные выводы предыдущих разделов.
1. Спектральная плотность средней мощности фазового шума на выходе цифрового делителя частоты при воздействии аддитивного шума на опорный сигнал на его входе описывается выражениями (15, 16). Эти выражения учитывают нелинейный характер зависимости и справедливы как для низкочастотных, так и для высокочастотных аддитивных воздействий на опорный сигнал. С их помощью можно не только качественно, но и количественно оценить мощность и спектральный состав фазового шума.
2. При проектировании цифрового синтезатора частот следует:
(a) обеспечить надлежащее экранирование, разместив блок синтезатора в отдельной секции и снабдив опорный сигнал и сигнал обратной связи защитными металлизированными полигонами на печатной плате;
(b) обеспечить фильтрацию опорного сигнала и, если целесообразно, сигнала обратной связи;
(c) если возможно, использовать одну и ту же частоту сравнения для синтезаторов, размещенных на одной плате;
(d) при необходимости выбрать промежуточную частоту сигнального тракта таким образом, чтобы минимизировать влияние наводок на опорный сигнал синтезатора.
3. На этапах отладки и тестирования обязательно следует обратить внимание на наводки на линию сигнала опорной частоты и сигнала обратной связи.
Приведенные результаты анализа и понимание сути описанного процесса помогут достигнуть более высоких характеристик разрабатываемого оборудования и существенно сократить время отладки и тестирования.
[1] Best, Roland E., Phase Locked Loop Teory, Design, and Applications, 3rd ed, McGraw-Hill, 1995
[2] Lascari, Lance Accurate Phase Noise Prediction in PLL Synthesizers, Applied Microwave & Wireless, Vol.12, No. 5, May 2000
[3] Emad Hegazi, Jacob Rael & Asad Abidi. The Designer’s Guide to High- Purity Oscillators. Springer, 2004